Weingarten map
It is the differential of the Gauss map $N$:
$$ p\in S \longmapsto \left\{dN_p:T_pS\rightarrow T_{N(p)}\mathbb{S}^2\right\} $$For every $p$, $dN_p$ transforms a little circle in $T_pS$ in an ellipse in $T_{N(p)}\mathbb{S}^2$, and is an useful way to measure extrinsic curvature. Indeed, since $dN_p(X)$ measures how it changes $N(p)$ in the direction $X$ (think of $dN_p(X)=\frac{d}{dt}(N\circ \alpha_X(t))$) and $N(p)$ has constant module equals to 1, it turns out that $dN_p(X)$ is orthogonal to $N_p$ itself, so $dN_p(X) \in T_{f(p)} f(S)$. So we can think about the Weingarten map as
$$ dN_p:T_pS\rightarrow T_{f(p)} f(S) $$It let us to speak about principal directions and principal curvatures (see the picture below obtained from a [Youtube video](https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwjB7fybh633AhVLUxoKHfZFDjEQtwJ6BAgHEAI&url=https%3A%2F%2Fwww.youtube.com%2Fwatch%3Fv%3Dmas-PUA3OvA&usg=AOvVaw3Yvk2NUJGThCkggFKzJBjR)):
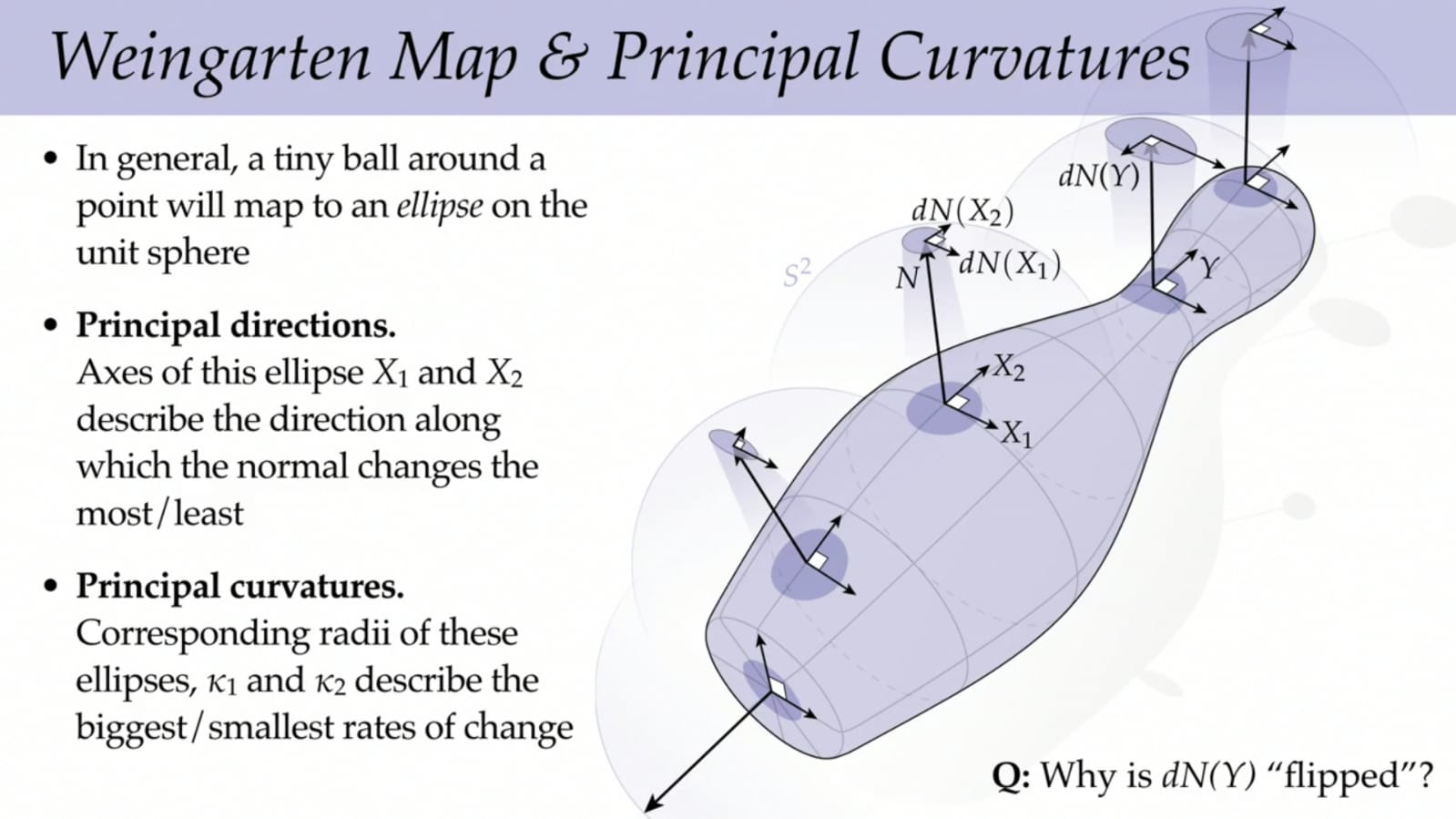
From the Gauss map we can define the normal curvature of an immersed surface.
The Weingarten map is related to the shape operator.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: